明捷數學漫談：挑戰極限的人（1）

《明捷數學隨談：挑戰極限的人（1）》

By 明捷

明捷是我的高中同學，跳級來到我們高中的尖子班，學霸。令人矚目的是數學成績格外突出，這一定有遺傳的因素，明捷的父親是大學數學教授，母親是高中數學教師。在1980年的高考中，明捷的成績名列前茅。他就讀於中國科技大學，後來又在中美兩國獲得碩士和博士學位。目前他在最著名的汽車公司工作，業餘時間，還會對數學念念不忘。在高中微信群里，他寫了一些在數學領域挑戰極限的人和事，十分有趣，大家建議他整理成文，發表出來，讓更多的人看到。不負眾望，一篇《明捷數學隨談：挑戰極限的人》一文，應運而生了。他沒有註冊任何網站，我就受他之託，將此文分享給大家。下面就是全文之一

【一．純數學】

上世紀一位數學權威，英國劍橋大學教授哈代曾說過：「大體上講，有用的數學都是膚淺的數學」。這裡說的「有用的數學」大概是指應用數學。哈代的言下之意是，只有純數學才是數學家真正的競技場。其暗含的意思也是相當殘酷的，即獻身純數學的數學家有可能一生離群索居，窮困潦倒，因為他們做的東西短期內沒有應用價值，大多數情況下都不會引起社會關注，不會帶來經濟收益。他們中間的幸運者，年青時在大學和專業研究機構謀到穩定的職位，生活雖不富有，卻很舒適，能夠一生專註於純數學研究。但並非所有人都有這樣的幸運。

【二．數論與歌德巴赫猜想】

數學中古老的難題大都與數論相關，其表述很淺顯，具有初中數學知識就可以明白，但嚴格證明卻極其困難。如我們這一代人耳熟能詳的哥德巴赫猜想，表述為：任何一個大偶數都可以寫成兩個素數之和。如8＝3+5，48＝17＋31，等等，如果有時間和耐心，可以一直驗算下去，直至幾十億，幾百億，但這樣驗證的數字再大，都不能證明該猜想。著名數學家陳景潤嘔心瀝血，一生的時間和精力都放在哥德巴赫猜想上，仍沒能證明它。但他取得了迄今世界上最領先的成果，證明了：任何一個大偶數都可以表示為一個素數和不超過兩個素數的乘積之和。如6=2+2×2，8=2+2×3，10=3+7等等。

1977年，作家徐遲發表的長篇報告文學《哥德巴赫猜想》，在民間引發了巨大的反響。這篇長文不僅讓人們知道了陳景潤這個悲情數學家，也讓人知道還有報告文學這樣一種寫作方式，更讓當時的有志青年們了解到人生除了走革命道路外，還可以選擇鑽研數學，成名成家。停頓十年後於當年恢復的高考，數學系得到了最好的生源。只是不知道當年報考數學系的高材生們，有多少人最後選擇了數學研究作為他們的終生職業。

【三．懷爾斯與費馬大定理】

中國古人在研究直角三角形時發現了＂勾三，股四，弦五＂，即3²+4²=5²。其實還有很多類似的邊長為整數的直角三角形，如（5，12，13），5²+12²=13²。西方人將勾股定理稱為畢達哥拉斯定理。300多年前，法國數學家費馬想在畢達哥拉斯定理的基礎上玩點數字遊戲，他想如果該等式的冪次不是二次，而是更高次，會不會也存在類似二次時的三整數組合來滿足方程呢？例如在方程a³+b³=c³中，是否存在a，b，c同為整數的解呢？他嘗試後，發現找不到整數解。在更高次下，同樣沒找到整數解。經過反覆思考後，他提出：在方程aⁿ+bⁿ=cⁿ中，當n>2時，不存在a，b, c同為整數的解。他在一本書的邊框上寫下了一段話，聲稱他找到了一個很妙的方法來證明這個定理，但證明過程寫不下。後來人們習慣上將這個定理稱為費馬大定理。接下來的300多年，一代又一代的數學家費盡心思，都無法證明這個定理。他們普遍認為費馬當年所說的那個＂很妙的證明＂一定是錯的。

轉眼到了19世紀末，一位年輕的德國企業家為情所困，決定自殺。自殺前的那天晚上，他莫名其妙地想去證明費馬大定理，整整一個通宵，突然發現已經錯過了原定自殺的時間，於是放棄了自殺方案。1908年，他臨終時囑咐從遺產中拿出10萬馬克，懸賞在接下來100年中能夠證明費馬大定理的人。

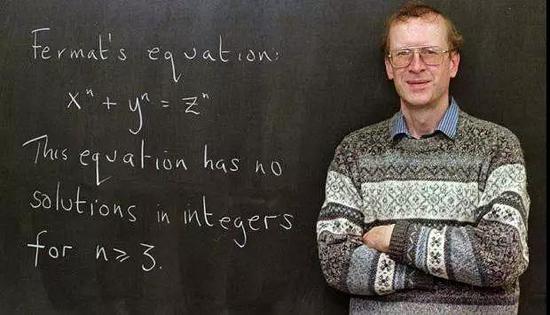
20世紀中葉，英國一個學童偶然知道了費馬大定理，鬼使神差地立志要證明它，他就是安德魯. 懷爾斯(Sir Andrew John Wiles，出生於1953年4月11日)。成年後，他理所當然地選擇數學為終生職業。多年以後，他任教於普林斯頓大學，住在家裡的閣樓上研究費馬大定理，只有他的妻子知道他在幹嘛。1993年，他聲稱證明了該定理，但證明過程公布後，被人指出存在缺陷。接下來一年時間，他都在致力於完善該證明。突然有一天，腦海中靈光閃現，一個簡潔漂亮的想法出現了。多年後他面對採訪者回憶當時的情形，仍抑制不住激動。他說當時整整一天，他都沉浸在難以描述的美感之中。他的證明終於被舉世公認。懷爾斯對數學的最大貢獻是證明了歷時350多年的、著名的費馬猜想。

順便說一句，和所有的研究成果一樣，懷爾斯的成就是因為站在前人的肩膀上。對懷爾斯影響最大的是上世紀50年代日本青年數學家谷山的研究工作。不幸的是，谷山年紀輕輕就突然自殺，隨後，他的未婚妻也自殺殉情。純數學領域部分從業人員的生存狀態，也許由此可見一斑。

【四．拉馬努金的公式】

1887年，印度南部一個叫拉馬努金的婆羅門家族出生了一個男嬰。以後發生的一切表明，這個孩子是專門為數學而生的。婆羅門在印度種姓制度中屬最高一級，但並不意味著他們都富有。事實上，這個家庭就屬於貧困一類的。當小拉馬努金快10歲時，已經完全沉浸在對數學的興趣中。這時家裡住進兩個大學生租客，小男孩一有空就去找這兩個大學生討論數學問題。很快，大學生的數學知識就不足以應付他了。他們甩給小拉一本《高等三角學》，說這本書我們也有不明白的，你自己去讀吧。小拉很快就研究完了這本書，他發現正弦和餘弦函數不僅是直角三角形中直角邊和斜邊之比這麼簡單，他們和自然對數的底以及單位虛數之間存在一個奇妙的關係，小拉當時不知道的是，這其實就是著名的歐拉公式，150年前就被大數學家歐拉發現了。後來小拉又得到一本叫做古今公式大全的書，列舉了幾千個數學公式，他整天忙著證明推廣這些公式。

轉眼要考大學了，小拉連著兩年都沒考上，第三年總算考進了一所大學，但因為嚴重偏科，掛了多門課，被學校勸退了。那時他的唯一財富就是一本厚厚的筆記，裡面寫滿了他自己發現的公式。他抱著這個筆記本四處找工作，卻沒人把它當回事。後來，他託人將筆記拿給當時印度數學學會的會長，會長也看不懂。但憑直覺，他意識到這個年輕人非同尋常。會長的正式職業是稅務局的官員，他將拉馬努金安排進稅務局，這是個閑職，即解決了小拉的財務困境，又能給他足夠的時間研究數學。

隨著拉馬努金在印度數學界名氣的增大，有人建議他到英國深造。他給當時的幾個英國數學權威寫信自薦，其中包括劍橋大學教授哈代。哈代看到他的那些公式，立即決定邀請他去劍橋。與拉馬努金見面後，哈代進一步了解了他作的研究，驚為天人。他形容和拉馬努金的相識，是「生命中的一次浪漫」。由於拉馬努金沒有經過系統的專業訓練，即使在數學領域，他的知識也是殘缺的，但這並不影響他成為一個偉大的數學家。他憑直覺寫下的那些公式，令人匪夷所思。當時很多人驚奇他是怎麼想到這些公式的，他說是睡夢中神給他的啟示。我第一次看到拉馬努金的那些公式時，感覺就是兩個字：震撼。一種謙卑感從心底由然而生。感覺到還存在另一個我毫無所知的數學世界，而拉馬努金就是從那個世界穿越過來的人。有人用「宏偉的公式」形容拉馬努金的作品，毫不過分。遺憾的是，早年的貧困生活和過度專註的研究，毀壞了拉馬努金的身體，使他在32歲時就離開了人世。

值得一提的是，數學公式通常都是經過嚴格推導得出。但拉馬努金的那些公式，都是他直接寫出來的，沒有推導過程。有人後來試圖證明他的一些公式，發現都是對的。但他寫下的公式太多了，還有很多留待後人證明。後來人們創辦了一個數學期刊，稱為《拉馬努金雜誌》，用來發表與他那些公式相關的研究工作。

愛因斯坦的一句話在拉馬努金的身上得到了驗證：想像力比知識更重要。或許人們無法擁有像拉馬努金一樣的直覺，但是，只要我們能夠放飛自己的想像里，看到的世界一定更加美好！

(照片來自網路）